Veremos en esta sección algunas subrutinas y sus algoritmos que tienen especial interés, por su uso cotidiano en las áreas de investigación o por el tema particular en el que se las utiliza.
La generación de números al azar es muy útil en muchos campos de la
ciencia, pero su uso supera al tema científico. Por ejemplo: dados,
mazos de cartas, ruletas, ruedas de la fortuna con premios anotados,
bolilleros para los sorteos de los temas de concursos, sorteos con
papelitos en una bolsa, sistemas de lotería estatales. Todos estos no
son más que ingenios mecánicos para generar un resultado que se supone
que es por azar. Por otro lado, los juegos del celular o de la
Playstation tienen que generar un sistema de azar para que el monstruo
que nos persigue cuando jugamos no repita el mismo esquema una y otra
vez, y el juego no termine resultando aburrido y tedioso.
A los números al azar se los suele denominar como números random o
aleatorios. Se pueden construir generadores de números al azar
utilizando computadoras, pero estos no generan secuencias infinitas,
sólo una secuencia inicial finita de números es estadísticamente
azarosa. Aunque esta secuencia pueden ser muy larga, se llega a un punto
en que los números se repiten y la secuencia deja de ser formada con
valores al azar. Esta área es un tema de investigación actual y existen
muchos algoritmos muy diferentes para realizar esta tarea. Por lo cual
esta explicación debe ser tomada como una introducción muy simple al
área. Pero sirve orientar en la complejidad y usos de estos
números.
En ciencia se usan mucho estos algoritmos para realizar simulaciones de
procesos físicos. Por ejemplo, simular observaciones con sus errores
para luego aplicarle los procesos de reducción y análisis de datos, con
el fin de comparar los resultados con los datos originales, entre muchos
otros usos. Otro ejemplo, es el de calcular las probabilidades de
observación de un fenómeno físico desde cierta perspectiva en
particular. A este último tipo de cálculo se lo llama método de Monte
Carlo. A los modelos realizados con estos números al azar se los suele
llamar “realizaciones”.
Veamos un método para generar una secuencia de números al azar, este
algoritmo venía programado en varias generaciones de calculadoras de la
empresa Texas Instruments. Pero primero recordamos que el resto de una
división se lo suele llamar módulo, es decir el resto de A divido B,
seria el \(A\ mod(B)\). El módulo
existe en Fortran como función intrínseca y suele utilizarse en los
generadores de números al azar. Estos generadores dan un secuencia de
números que los denominaremos: \(X_0\),\(X_1\), \(X_3\),...,\(X_N\) y para generarlos usamos el siguiente
algoritmo:
\[X_{i+1} = \frac{(A X_i +
C)mod(M)}{M}\]
Es decir, con el valor al azar \(X_i\)
construimos el número al azar que sigue \(X_{i+1}\). Al primer \(X\) de la secuencia (el \(X_0\)) hay que asignarlo, es decir no
proviene del algoritmo y con él se inicia la secuencia. A este primer
número se lo llama la semilla. Muchas veces se prefiere que la semilla
sea fija, para que se repita la secuencia igual, pero si lo que importa
es que la secuencia sea siempre diferente (como en un juego) se cambia
la semilla en cada comienzo de la simulación, para que cada corrida del
programa se realice con diferentes números. En los juegos muchas veces
se usa el reloj de la computadora (recordar que el celular, como la
Nintendo o la Playstation son computadoras y tienen un reloj interno)
para tomar el tiempo con muchos decimales y con el fin de usarlo como la
semilla que inicia una nueva secuencia.
Note que con este algoritmo hacemos una cuenta y a ese resultado le
tomamos el mod(M) o sea nos quedamos con el resto de la división por M.
El resto no puede ser mayor que el divisor (M) y si después lo dividimos
por M, nos quedan números en el intervalo \([0,1)\). Por lo tanto, nuestra secuencia de
números al azar está siempre en ese intervalo.
En este algoritmo A, C y M tienen números prefijados que se conocen por dar secuencias bastante largas. La razón de que las secuencias de números al azar se agoten se debe principalmente a la pérdida de decimales por el redondeo en las operaciones de punto flotante.
La subrutina sería así:
\(\ \ \ \ \ \ \ \) Subroutine
azar(X)
\(\ \ \ \ \ \ \ \) real*8 X
\(\ \ \ \ \ \ \ \) integer A,C
\(\ \ \ \ \ \ \ \) A = 24298
\(\ \ \ \ \ \ \ \) C = 99991
\(\ \ \ \ \ \ \ \) M = 199017
\(\ \ \ \ \ \ \ \) X = MOD(X * A + C,M) /M
\(\ \ \ \ \ \ \ \) return
\(\ \ \ \ \ \ \ \)
end
Esta rutina nos dará números al azar con una distribución uniforme, es
decir, cualquier número tiene la misma probabilidad de aparecer que
otro. Existen algoritmos para otras distribuciones, como por ejemplo,
una campana de Gauss, etc, donde ahora algunos números son más probables
que otros. Si se quisiera que los números estén en algún otro intervalo
como en una ruleta, siempre se puede hacer un cambio de escala lineal
para moverlos sin que estos cambien sus propiedades. Es decir, estoy en
el intervalo \([0,1)\) y quiero pasar
al intervalo \([A,B)\) simplemente
calculo mi nueva secuencia haciendo \(X^* = X
* (B - A) + A\). Por ejemplo, si quisiera imitar una ruleta mi
nueva secuencia tendría que estar en el intervalo \([0,37)\). Por lo tanto, la secuencia que
imitaría a la ruleta sería \(X^* = X * 37
+ 0\). Y consideraría que el valor entero de \(X^*\) es el valor que sale de cada jugada
de la ruleta virtual.
Con la subrutina que genera números al azar, veremos una manera de calcular el número \(\pi\). Pero primero repasaremos en modo sucinto algunos conceptos de teoría de probabilidades. Se denomina frecuencia a la cantidad de veces de que un cierto estado se repita en un experimento frente a todos los experimentos que se han realizado. La frecuencia es algo que se puede medir. Por ejemplo, tirando una moneda y contando la cantidad de veces que sale cara frente a las veces que esa moneda fue arrojada.
La probabilidad de que ese estado en particular suceda es un
resultado teórico que se obtendría de repetir infinitamente el
experimento. La frecuencia entonces se convierte en probabilidad cuando
el número de experimentos tiende a infinito. En este caso vamos a asumir
que cuando repito mucho veces un experimento y mido la frecuencia se
parecerá bastante a la probabilidad. Es decir, puedo tirar una moneda
muchas veces al aire, y medir la frecuencia de que salga cara y no seca.
Pero sólo cuando se la tire infinitas veces obtendré la probabilidad del
suceso.
Pero como la probabilidad es una definición: prob= casos
favorables/casos totales, para una moneda perfecta tengo: una cara/dos
posibilidades (cara mas seca). O sea que la probabilidad de obtener cara
es \(Prob= 0.50\).

Con esta explicación vamos a calcular la probabilidad de un
experimento curioso, que es el siguiente:
Tengo un cuadrado perfecto dibujado en el piso y le arrojo piedras. Si una piedra cae afuera la vuelvo a tirar.
Tengo un contador que lleva la cuenta de todas las piedras que se arrojan.
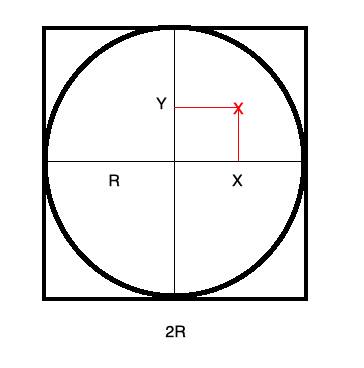
Dentro de ese cuadro dibujo un círculo centrado y con el radio tal de que es tangente a todos los lados de cuadrado. Ver dibujo 1.1 .
Llevo la cuenta de todas piedras que caen en el círculo.
Realizo este experimento utilizando la computadora. La posición de la piedra la determino generando dos números al azar con distribución uniforme. Es decir la coordenadas (x,y) del impacto de la piedra son dos números al azar.
Repito el experimento muchas veces, con la idea de que cuando más veces mejor (¿Esto será bueno?)
Calculo la frecuencia de que la piedra caiga dentro del círculo.
Es decir:
\(frec= \frac{piedras\ en\ el\
c\acute{i}rculo}{total\ de\ piedras}\)
Viendo este experimento ¿Cuál es la probabilidad de que una piedra
quede dentro del círculo?
\[Prob = \frac{Casos\ favorables}{Total\ de\
casos} = \frac{\acute{A}rea\ del\ c\acute{i}rculo}{\acute{A}rea\ del\
cuadrado}\]
Reemplazando áreas por su expresiones y haciendo las cuentas
\[Prob = \frac{\pi R^2}{(2R)^2} = \frac{\pi}{4}\]
Si suponemos (aunque sabemos que se le parecen pero no son lo mismo) que la frecuencia medida es la probabilidad de que la piedra caiga en el círculo, obtenemos que:
\(frec \sim \frac{\pi}{4}\) y si despejo \(\pi\) obtengo \(\pi \sim 4 frec\) donde la frecuencia la obtengo a partir de la simulación. Pero para que esto funcione tenemos que hacer que la frecuencia realmente se parezca a la probabilidad y para que esto suceda tenemos que repetir el experimento muchas veces (¡quizás varios millones de veces!).
Veamos cómo sería un programa que realice toda esta tarea. Genere los dos números al azar, vea si estás coordenadas están dentro del círculo, actualice los contadores (piedras en el círculo y cantidad total de piedras), nos de un estimado del valor de \(\pi\) que obtuvimos hasta el momento y vuelva a repetir la operación una y otra vez.
\(\ \ \ \ \ \ \ \)program pi_con_azar
c Inicializo
\(\ \ \ \ \ \ \ \)real*8 x,y,xf,pi,puntos,puntosc
c xf es la semilla recomendada para una serie muy larga de números al azar en
c este generador
\(\ \ \ \ \ \ \ \)xf=0.3846293861039840D15
\(\ \ \ \ \ \ \ \)n1=0
\(\ \ \ \ \ \ \ \)puntos=0.
\(\ \ \ \ \ \ \ \)puntosc=0.
\(\ \ \ \ \ \ \ \)
c Calculo la simulación de arrojar una piedra y la cuento en “puntos”
c Si cae dentro del círculo, además la cuento en “puntosc”
10 \(\ \ \ \)continue
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)call azar(xf,x)
\(\ \ \ \ \ \ \ \)call azar(xf,y)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)puntos=puntos+1
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)if (x**2+y**2.le.1) then
\(\ \ \ \ \ \ \ \ \ \)puntosc=puntosc+1
\(\ \ \ \ \ \ \ \)endif
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)pi=puntosc/puntos*4
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)n2=puntos/1000000
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)if(n2.gt.n1) then
\(\ \ \ \ \ \ \ \ \ \ \)call escribir(n2,pi,puntos)
\(\ \ \ \ \ \ \ \ \ \ \)n1=n2
\(\ \ \ \ \ \ \ \)endif
\(\ \ \ \ \ \ \ \)goto 10
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)end
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)subroutine escribir(n2,pi,puntos)
\(\ \ \ \ \ \ \ \)real*8 puntos,pi
\(\ \ \ \ \ \ \ \)error=1./sqrt(puntos)
\(\ \ \ \ \ \ \ \)write(*,*) ’pi=’,pi,’ con ’,n1,’millones de puntos con un error
\(\ \ \ \ \ \)#de’,error
\(\ \ \ \ \ \ \ \)return
\(\ \ \ \ \ \ \ \)end
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)SUBROUTINE AZAR(Y,X)
\(\ \ \ \ \ \ \ \)REAL*8 X,Y
\(\ \ \ \ \ \ \ \)Y=65539D0*Y
\(\ \ \ \ \ \ \ \)Y=DMOD(Y,2147483647D0)
\(\ \ \ \ \ \ \ \)X=Y*4.65661287524D-10
\(\ \ \ \ \ \ \ \)RETURN
\(\ \ \ \ \ \ \
\)END
La subrutina escribir() se encarga de justamente
imprimir en pantalla el valor parcial de \(\pi\) conseguido hasta el momento. Es
llamada cuando el valor del número de simulaciones cambia el dígito del
millón. De esa manera se consigue que el programa funcione más rápido.
Escribir en pantalla consume muchos recursos de la computadora y en este
caso no es necesario que se haga todo el tiempo. Y esos recursos van
ahora a ser usados en que la simulación corra más rápido.
El error en la simulación se lo considera como Poissoniano (cumple con
la distribución de Poisson) y por lo tanto para N eventos el error
relativo es \(error=1/\sqrt{n}\).
La tabla 1.1 son los resultados para distintas cantidades de simulaciones de piedras arrojadas.
| # de piedras | Valor de \(\pi\) obtenido | Error estadístico |
|---|---|---|
| \(10^6\) | 3.1424319999999999 | \(1.00000005\ 10^{-3}\) |
| \(10^7\) | 3.1407848888888887 | \(3.33333330\ 10^{-4}\) |
| \(10^8\) | 3.1416244799999999 | \(9.99999975\ 10^{-5}\) |
| \(10^9\) | 3.1415663320000000 | \(3.16227779\ 10^{-5}\) |
| \(10^{10}\) | 3.1416044472000002 | \(9.99999975\ 10^{-6}\) |
| \(10^{11}\) | 3.1415875904799999 | \(3.16227761\ 10^{-6}\) |
| \(10^{12}\) | 3.1415921563320000 | \(9.99999997\ 10^{-7}\) |
| \(10^{13}\) | 3.1415922104799999 | \(3.16227761\ 10^{-7}\) |