Existen varios tipos de Variables Numéricas utilizadas en los
sistemas digitales, pero antes de prestar atención a sus características
es necesario discutir un punto que es importante al usar computadoras.
Estas difieren en como se representan internamente los números con
respecto a cómo lo hacemos nosotros los humanos. Esto es debido a que
las computadoras trabajan en base binaria (base 2) y no en base decimal
(base 10).
¿Cómo es esto?
Las computadoras utilizan señales eléctricas para transportar, procesar
y guardar la información. Es decir, tienen cables metálicos que llevan
pulsos de corriente eléctrica. El pulso o la falta de este en el momento
adecuado es usado como información. Entonces, si hay un pulso eléctrico
en un cable lo anotamos con un 1 y si no lo hay con un 0. Como sólo
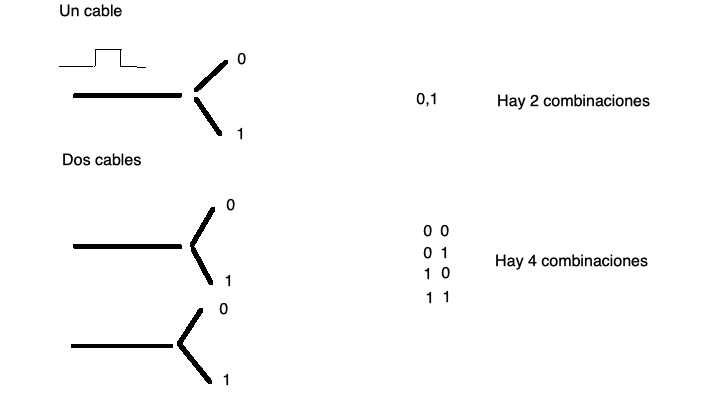
están estas dos posibilidades hablamos de un sistema binario. Supongamos
que tenemos un sólo cable, bueno sólo puedo tener dos números el 0 y el
1, esta configuración se la llama bit (ver fig. 1.1). Un sólo cable no es muy útil, sólo
tenemos un sistema que puede representar dos números. La forma de
resolver esta situación es la de agregar más cables. Veamos entonces que
sucede si agregamos un cable más. Con dos cables tendremos 0,0 (ambos
cables sin un pulso eléctrico), 0,1 y 1,0 (si uno tiene el pulso y el
otro no) o 1,1 (en el caso que los dos cables lleven un pulso
eléctrico). Es decir, con dos cables se obtienen 4 configuraciones
diferentes que me permiten representar 4 números. Es obvio entonces que
agregando más cables puedo representar más números. La tabla 1.1 describe lo que va pasando a
medida que agregamos más cables.

| Cantidad de Cables | Cantidad de números | Potencia de 2 ( \(2^n\)) |
| N (bits) | que puedo escribir | |
| 1 | 2 | 1 bit \(\rightarrow\) \(2^1=2\) |
| 2 | 4 | 2 bits \(\rightarrow\) \(2^2=4\) |
| 3 | 8 | 3 bits \(\rightarrow\) \(2^3=8\) |
| 4 | 16 | 4 bits \(\rightarrow\)\(2^4 =16\) |
| ... | ... | ... |
| 8 | 256 | 8 bits \(\rightarrow\)\(2^8=256\) \(\leftarrow\) Byte |
| ... | ... | ... |
| 10 | 1024 | 10 bits \(\rightarrow\)\(2^{10}=1024\) \(\leftarrow\) Kilobits [Kb] |
| ... | ... | ... |
| 20 | 1048576 | 20 bits \(\rightarrow\)\(2^{20}=1048576\) \(\leftarrow\) Megabits [Mb] |
| ... | ... | ... |
| N | M | N bits \(\rightarrow\)\(2^N=M\) |
| Símbolo | Prefijo | MKS | Binario | Diferencia Porcentual | Ref |
|---|---|---|---|---|---|
| K | kilo | \(10^3 = 1000^1\) | \(2^{10} = 1024^1\) | 2.40% | |
| M | mega | \(10^6 = 1000^2\) | \(2^{20} = 1024^2\) | 4.86% | Memoria Cache |
| G | giga | \(10^9 = 1000^3\) | \(2^{30} = 1024^3\) | 7.37% | Memoria RAM/SSD |
| T | tera | \(10^{12} = 1000^4\) | \(2^{40} = 1024^4\) | 9.95 % | Discos Rígidos/SSD |
| P | peta | \(10^{15} = 1000^5\) | \(2^{50} = 1024^5\) | 12.59% | Grandes Servers |
| E | exa | \(10^{18} = 1000^6\) | \(2^{60} = 1024^6\) | 15.29% | Datacenters/Nube |
| Z | zetta | \(10^{21} = 1000^7\) | \(2^{70} = 1024^7\) | 18.06% | |
| Y | yotta | \(10^{24} = 1000^8\) | \(2^{80} = 1024^8\) | 20.89% |
En la tabla 1.1 se puede ver la definición de
Byte (B en mayúscula) frente a la de bit (b en minúscula). Recordar que
un Byte son 8 bits, por ejemplo: 1110001 o 00011111.
El Byte es la unidad de memoria de información en las computadoras.
Ejemplos: la memoria se mide en Gigabytes (mil millones de Bytes), los
discos rígidos en Terabytes (millón de millones de Bytes). Por ejemplo,
la velocidad de conexión a internet puede ser medida en unidades de
bit/segundo o Bytes/segundo. Pregunta inquietante para resolver: ¿Qué
velocidad tienen en la conexión a internet en sus hogares? ¿Cuánto en
Bytes y cuánto en bits? ¿Es simétrica? Es decir ¿La bajada de
información de la red tiene una velocidad igual a la subida?
También hay que notar que se usan unidades parecidas al MKS, pero
no son iguales en tamaño, un kilo MKS es \(1000=10^3\) pero un Kilobyte es \(1024=2^{10}\). No es la misma relación. Lo
mismo para un megabyte \(1048576 =
2^{20}\) que no es \(10^6\) como
son las unidades MKS. La tabla 1.2 nos
muestra como las notaciones binarias y decimales difieren cuando los
números se vuelven más grandes, aunque los nombres que se usan en los
dos sistemas de unidades son los mismos. Esta situación es causante de
muchas confusiones.
En un intento de resolver la falta de claridad de estas unidades, la
Comisión Electrotécnica Internacional (IEC) en diciembre de 1998
estableció el estándar de almacenamiento de 1024 bytes con la
nomenclatura de KiB en vez de kB como era anteriormente y denominarlo
kibibyte, para diferenciarlo del kilobyte. Por lo cual, 1 kibibyte =
1024 B = \(2^{10}\) bytes y 1 kilobyte
= 1000 B = \(10^3\) bytes. Si bien esta
comisión establece los estándares internacionales, lo que terminó
creando fue una mayor confusión, ya que esta unidad nueva es muy poco
usada e incluso grandes empresas la ignoraron por completo (por ejemplo:
Microsoft, Apple la usa en forma parcial, etc). Tampoco en el área de la
astronomía o en la ciencia en general esta nueva unidad ha tenido algún
éxito y esta forma de notación no es usada.
Cuando uno habla de base numérica se refiere a que si uso base 10, es 10
justamente el primer número que tengo que componer utilizando caracteres
ya existentes (en este caso el 1 y 0). En binario, que es base 2, es
entonces el número “2” el que se escribe como 10 en esa base. El número
45 en base 10 se sobreentiende que es \(4 x
10^1 + 5 x 10^0 = 45\) (note como la base es la que caracteriza
el orden de magnitud de los dígitos), pero en binario este número sería:
101101, ya que \(1 x 2^5 + 0 x 2^4 + 1 x 2^3 +
1 x 2^2 + 0 x 2^1 +1 x 2^0 = 32 + 8 + 4 + 1 = 45\)
Otra de base que se usa mucho en computación, tecnologías
electrónicas y digitales es la base 16 o hexadecimal. Por lo que
explicamos antes, en esta base el 16 se escribe como el número 10. En la
tabla 1.3 hacemos la conversión entre
diferentes bases para los primeros 16 números naturales.
| Número Decimal | Binario | Hexadecimal |
| Base 10 | Base 2 | Base 16 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Por convención, los números hexadecimales se los escribe con un “0x” delante para indicar la base 16. Por ejemplo, 0x9AD3 o 0x45FC ¿Cuál sería entonces, la ventaja de usar número en una base tan “antinatural” (por decirlo de alguna manera) como es la base 16? Hay una razón simple y es la siguiente: 4 bits (o sea medio Byte) describe todos los números posibles entre 0 y 15 (ver la tabla 1.1) entonces 1 Byte puede ser escrito como dos números hexadecimales. Por ejemplo, el numero binario 10011111 se podría escribir como 0x9F (1001 \(\rightarrow\) 9 y 1111 \(\rightarrow\) F) y esto evita un problema importante que tienen los números binarios, ya crecen muy rápidamente en la cantidad de dígitos cuando los números son grandes y por lo tanto se vuelven complicados de escribir, recordar, etc y en general, de manejar. Con los hexadecimales sucede la situación inversa, para un mismo número su escritura es más corta en cantidad de dígitos que su versión decimal y todavía mucho más corta que la representación binaria, con la ventaja de la correspondencia directa que tienen con los números binarios.
El Byte es la definición de la unidad de memoria y proceso de una computadora, por lo tanto sólo, se puede utilizar una cantidad entera de Bytes en cualquier proceso digital. No existen ni se usan las fracciones de Bytes. Es básicamente el ladrillo con que se construyen las unidades de información (más delante esta idea quedará más clara) en los sistemas digitales.
En los sistemas de computación, la forma de manejar los distintos tipos de números (enteros, reales, etc.) dependen de una combinación de Hardware y Software. Mientras las operaciones matemáticas básicas la realiza el Hardware en la CPU, la definición completa de las atribuciones de los números depende del Software a usar. Dicho de otra manera, cada lenguaje de computación tiene algunas definiciones diferentes de las propiedades de los números que usa. Veremos en este curso cómo los números binarios se usan para construir los distintos tipos de variables numéricas en los Lenguajes FORTRAN y PYTHON.
Con los Bytes que vimos en la sección anterior se construyen los número que usamos en nuestros cálculos. Así como se ve en un curso de Análisis Matemático hay diferentes clases de números, por ejemplo, naturales, enteros, reales, complejos, etc, lo mismo pasa en los sistemas de computación. Veamos los tipos más comunes de construcciones numéricas y luego estudiaremos cómo se usan en cada lenguaje.
Los enteros (integer en inglés) utilizan típicamente de 4 u 8 Bytes
para su construcción, aunque muchos sistemas pueden usar a pedido del
usuario 2 Bytes o una cantidad mayor de Bytes (16 o más)
¿Cómo se usan estos bytes?
Cada Byte tiene 8 bits, y con estos se construyen en base binaria los
números. Estos pueden tener o no tener signo (unsigned en inglés) y
serían solo los números positivos (naturales) o con signo (signed), que
serían los números enteros tal cual se definen en un curso de
matemática. Si el número es unsigned y tengo 4 Bytes (32 bits) podrían
escribirse \(2^{32}\) números, que
estarían comprendidos en el intervalo [0, 4294967295]. En cambio, si es
signed tendré que usar uno de los bits para indicar si el número es
positivo o negativo, quedándome con 31 bits para escribirlo. Con estos
31 bits puedo construir \(2^{31}\),
pero cómo tengo positivos y negativos me quedan los números entre estos
valores [-2147483648, 2147483647].
Como ya aclaramos, se pueden usar más o menos Bytes para representar el
número entero. En la tabla 1.4 vemos
para diferentes usos de los Bytes y los intervalos de números que
logramos representar.
| Bytes | bits | Sin signo (unsigned) | Con signo (signed) |
| n | \(8 n\) | max. número (\(2^{8n}-1\)) | intervalo de números |
| 1 | 8 | 256 | [-128, 127] |
| 2 | 16 | 65535 | [-32768, 32767] |
| 4 | 32 | 4294967295 | [-2147483648, 2147483647] |
| 8 | 64 | 18446744073709551615 | [-9223372036854775808, 9223372036854775807] |
Las operaciones con números enteros se realizan en una unidad especifica para tal fin en la CPU. Eso significa que las operaciones básicas (suma, resta, multiplicación, división, etc) se realizan en esa unidad que es sólo para cálculos con números enteros. Hay que tener en cuenta que la división de enteros sólo puede dar como resultado otro número entero, perdiéndose la parte fraccionaria del número resultante de esta operación. Ejemplo, 7/3 da como resultado 7/3=2
Los números reales son más complicados en muchos sentidos, ya que se escriben internamente en la computadora en binario en forma de una mantisa y un exponente. Estos números se los llama flotantes debido a que el problema original de los ingenieros era que el punto decimal flotaba y podría estar en cualquier lugar del número. Pero en sí, esa no es la dificultad más importante, sino que los números reales pueden tener infinitos decimales y no existe tal cosa como memoria infinita en una computadora. En algunos casos los números reales deben ser cortados (o truncados), perdiendo los últimos dígitos de la parte fraccionaria, ya que no se pueden guardar. Veremos más adelante que esta pérdida de decimales trae consecuencias (malas!) en algunos cálculos donde la propagación de errores es importante, pero también que existen formas para disminuir el efecto de este problema. Estos flotantes se representan utilizando una cierta cantidad de bits (de los Bytes) distribuyéndolos en el signo del número, la mantisa y el exponente.
Básicamente, un número sería en binario: \(\pm mantisa\ x \ 2^{\pm exponente}\). La norma IEEE-754 utiliza 4 Bytes (32 bits) para los reales simples, donde 8 bits son para el exponente y los 24 restantes para la mantisa y el signo.
A veces en cálculos muy precisos esta representación de los números no alcanza, ya que se necesita una mayor cantidad de decimales significativos de los que usando. En esos casos se pueden usar reales de 8 Bytes (se los denomina como real*8 o doble precisión) con lo cual hay 64 bits para repartir entre mantisa y exponente. Las operaciones que se realizan con números real*8 conservan más decimales significativos. En algunos lenguajes de programación permiten definir real*16 (o sea 16 Bytes para escribir el número), pero estas variables no son las más comunes, ya que se necesita que el hardware pueda manejarlas. Definir números como real*8 o real*16 puede acarrear dos problemas: el primero es que se necesita más memoria para guardarlos y por lo tanto tiempo en esta tarea, y en el caso de real*16 mayor tiempo de cálculo. Las operaciones con números reales se realiza en las unidades de punto flotante de la CPU que es un circuito electrónico diferente del que realiza las operaciones con enteros. En el caso de real*8 se utilizarían entonces 64 bits, tomados de la siguiente forma: 1 bit para el signo, 11 para el exponente, y 52 para la mantisa. Esto significa que los valores que podemos representar van desde \(\pm2.2250738585072020 x10^{ -308}\) hasta \(\pm1.7976931348623157×10^{308}\).
En base a lo que vimos antes es importante señalar que si escribo 1.0 o 1. (sin poner el 0) este número es real, mientras que el 1 (sin el punto decimal) es un número entero. Las dos formas de representar el número como real o como entero no tienen la misma representación binaria dentro de la computadora.
Los números complejos se los considera como números con dos componentes reales y cada lenguaje tiene sus protocolos propios para describirlos. Las operaciones con números complejos están implementadas correctamente en los lenguajes que los soportan. Es decir, el sistema realiza operaciones sabiendo que \(i^2=-1\).
Si bien las computadoras realizan todas sus operaciones en binario,
los resultados son convertidos a notación científica al mostrarlos al
usuario cuando la situación lo requiera. Un caso de interés es como
muestran la notación científica ya que lo hacen indicando con la letra
E que lo que sigue del número es el exponente en base
10.
Ejemplos:
1E23 es el número \(1\ x\
10^{23}\)
4.345E03 es el número \(4.34\ x \
10^{3}\) o sea el 4340
También existe la posibilitad de que el exponente sea negativo así que
el número 24323E-45 es el \(24323\ x\
10^{-45}\) En Fortran, también se puede en vez de la E usar la
letra D, indicando que el número debe ser considerado tanto para
guardarse en memoria o en las operaciones matemáticas como doble
precisión (real*8).